Codage des couleurs
Programmation Python
Objectif
Qu'est-ce qu'un pixel ? Comment est représentée une couleur dans un ordinateur ? Voilà les questions que pose cette activité.
Cette activité s'inscrit dans la thématique La photographie numérique du programme de SNT.
Elle est proposée par Dominique Gluck, professeur de Sciences de l'Ingénieur au lycée Raoul Dautry à Limoges.
Capacités attendues
-
Distinguer les photosites du capteur et les pixels de l'image en comparant les résolutions du capteur et de l'image selon les réglages de l'appareil.
-
Traiter par programme une image pour la transformer en agissant sur les trois composantes de ses pixels.
Introduction
Cette séance a pour objectif de comprendre, à l'aide d'instructions Python, la structure d'une image numérique et le codage des pixels selon leurs composantes rouge, vert, bleu.
On s'exercera à jouer avec les couleurs à l'écran et à effectuer des traitements simples sur l'image.
La calculatrice NumWorks intègre un module graphique appelé kandinsky qui va nous permettre d'analyser et de définir la couleur de chacun des pixels de l'image (écran 320*222 points).
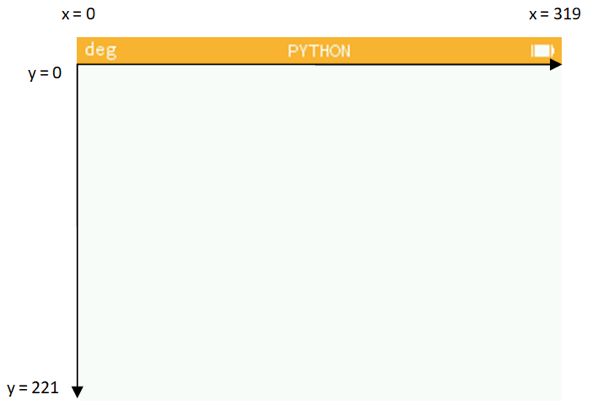
Découverte du codage des couleurs
On aura besoin ici de deux fonctions du module graphique kandinsky :
-
set_pixel(x,y,color): colore le pixel de coordonnées (x,y) de la couleur définie parcolor; -
color(r,g,b): définit une couleur en fonction de ses composantes rouge, vert, bleu.
-
À partir de l'écran principal, aller sur l'application Python (valider en appuyant sur ok. Faire défiler la page et ajoutez un script que l'on nommera
couleurs.py(valider par ok).Saisir ensuite le code suivant:
from kandinsky import * for y in range(25): for x in range(320): col=color(x,0,0) set_pixel(x,y,col) -
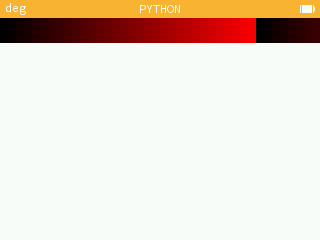
Exécuter le script. Qu'observe-t-on ?
On observe une barre de dégradé allant du noir au rouge. Le dégradé ne va pas jusqu'au bord de l'écran ; il semble qu'une nouvelle barre de dégradé débute à droite de l'écran
Quelques explications sur le programme :
-
xdésigne la position horizontale du point (abscisse),ysa position verticale (ordonnée) ; -
ligne 1 : on importe les fonctions graphiques du module
kandinsky; -
ligne 2 : on fait varier
yde 0 à 24 (boucle principale du programme) ; -
ligne 3 : on fait varier
xde 0 à 319 (boucle secondaire du programme).
Pour chaque valeur de y et x, on exécute les lignes 4 et 5 :
-
ligne 4 : on définit une couleur : ici l'intensité du rouge dépend de la position
x, l'intensité du vert et du bleu sont fixées à zéro. ; -
ligne 5 : on donne au pixel courant la couleur que l'on vient de définir.
La couleur du point dépend donc de la position x, d'où un dégradé sur la ligne horizontale ; on reproduit le tracé sur 25 lignes, d'où la création d'une bande horizontale de dégradé d'une hauteur de 25 lignes.
Nous allons tenter de répondre à la question suivante : pourquoi le dégradé ne s'étend-il pas sur l'ensemble de la largeur de l'écran ?
Le dégradé du noir vers le rouge s'étend sur les 4/5e de la largeur de l'écran, puis reprend à partir du noir. La couleur est définie par color(r,g,b) selon le système rouge, vert, bleu (RGB = red, green, blue) où les paramètres r, g, b sont des nombres entiers dont la valeur doit être comprise entre 0 et 255.
Cela vient du fait que la valeur de chacune des composantes rouge, vert, bleu est codée sur un octet. En effet, un octet est un nombre binaire de 8 bits valant chacun 0 ou 1, ce qui donne 256 combinaisons possibles.
Pour s'en convaincre, tapez dans la console bin(13) : la calculatrice affiche l'expression binaire (notée 0b) de 13 : 0b1011, on voit qu'il faut 4 bits pour coder en binaire le nombre 13 : 1011. En effet .
-
Combien de bits sont nécessaires pour coder 255 et 256 en binaire ? Pour répondre, tapez
bin(255)etbin(256)et relevez les expressions binaires correspondantes. -
Chaque point étant défini par ses trois couleurs et chaque couleur étant codée sur un octet, calculer en octets, puis en ko (kilo-octets), la mémoire nécessaire pour coder, selon ce principe, l'ensemble des points de l'écran de la calculatrice.
-
Editer le script
couleurset ajouter les lignes suivantes :for y in range(25,50): for x in range(256): col=color(0,255-x,0) set_pixel(x,y,col)Exécutez le script et observez l'écran. Que fait ce morceau de programme ?
-
Expliquez le fonctionnement du programme en commentant chaque ligne.
-
Compléter le programme pour créer une troisième bande de dégradé noir vers bleu et de longueur 256.
-
Créer une quatrième bande de dégradé noir vers jaune : le jaune correspond à une intensité égale du rouge et du vert ; le bleu est à 0.
-
Créer une cinquième bande de dégradé vert vers rouge.
-
Observons de près : la calculatrice paraît-elle produire réellement 256 niveaux dans chaque couleur ?
bin(255) = 0b 1111 1111 : 8 chiffres sont nécessaires.
bin(256) = 0b 1 0000 0000 : 9 chiffres sont nécessaires.
255 est bien la plus grande valeur que l'on peut coder sur 8 bits : .
Remarque : diverses solutions permettent de diminuer la taille du fichier nécessaire au stockage de l'image…
Il trace une barre de dégradés allant du vert au noir.

for y in range(25,50):
# pour les 25 lignes suivantes de l'écran
for x in range(256):
# pour x variant de 0 à 255
col=color(0,255-x,0)
# les niveaux du rouge et du bleu restent à 0
# le niveau du vert varie de 255 à 0 en fonction de x
set_pixel(x,y,col)
# on attribue la couleur au pixel de coordonnées (x,y)
On ajoute les lignes de code suivantes :
for y in range(50,75):
for x in range(256):
col=color(0,0,x)
set_pixel(x,y,col)

On ajoute les lignes de code suivantes :
for y in range(75,100):
for x in range(256):
col=color(x,x,0)
set_pixel(x,y,col)

On ajoute les lignes de code suivantes :
for y in range(100,125):
for x in range(256):
col=color(x,255-x,0)
set_pixel(x,y,col)

Non, on observe en fait une succession de bandelettes verticales à l'intérieur desquelles la couleur est homogène. L'observation de bandelettes verticales montre que la calculatrice ne produit en fait que 32 niveaux différents dans chaque couleur, ce qui constribue déjà à économiser la taille de mémoire nécessaire pour stocker l'image.
Drapeau
On cherche à dessiner le drapeau français.

Indications
-
Définir les couleurs : on donne
blanc=color(255,255,255). -
Colorier : on utilisera plusieurs boucles
for. Plusieurs méthodes sont possibles : soit tracer les 3 rectangles de couleur, soit tracer une ligne entière et la reproduire 222 fois. -
Créer le script
drapeau.py: Le tester, le mettre au point et faire vérifier.
Besoin d'aide ?
Si l'on adopte la deuxième méthode (balayage ligne par ligne) du dessin du drapeau, le script peut commencer ainsi :
from kandinsky import *
# definition des couleurs (a completer):
bleu=color(..., ..., ...)
blanc=color(255,255,255)
rouge=color(..., ..., ...)
# pour toutes les lignes :
for y in range(222): # y varie de 0 à 221
# partie gauche en bleu :
for x in range(0,107): # premier tiers de la ligne
set_pixel(x,y,bleu)
# milieu en blanc :
for x in range(108,215): # deuxieme tiers de la ligne
...
Si l'on adopte la première méthode (dessin de 3 rectangles), on peut définir une fonction : def rectangle(x,y,couleur) qui trace un rectangle de largeur 107 et de hauteur 222, où x> et y sont les coordonnées du point de départ et appeler trois fois la fonction rectangle(x,y,couleur).
Nuances de gris
-
Quelle est la couleur définie par
color(0,0,0)? -
Quelle est la couleur définie par
color(255, 255, 255)? -
En déduire comment définir un gris moyen. Testez.
Noir.
Blanc.
Les paramètres r, g, b, de la fonction color(r,g,b) doivent avoir les mêmes valeurs, par exemple : color(128,128,128).
Mire de gris
On veut écrire un programme permettant de partager l'écran en 10 bandes verticales de gris, allant du noir au blanc, le tout sur une hauteur de 100 pixels.
-
Quelle sera la largeur d'une bande ?
-
On veut que les intensités de gris soient bien réparties entre les valeurs extrêmes :
color(0, 0, 0)etcolor(255, 255, 255). Quelle valeur faut-il ajouter au paramètre de couleur pour passer d'une bande à sa voisine ? -
Saisir le script suivant. La structure du programme aura trois boucles imbriquées.
from kandinsky import * # pour les 100 lignes du haut : for y in range(100): # pour les 10 barres verticales: for b in range(10): # pour les 32 points horizontaux de chaque barre : for x in range(b*32,b*32+32): -
Compléter le script suivant (définition de la couleur du pixel) à la suite du précédent :
c=color(b*28,...,...) set_pixel(x,y,c) -
Variante: on veut que le dégradé aille du blanc au noir en allant de gauche à droite. Modifier la ligne
c=color(b*28, ..., ...).
pixels
28, car si la première nuance est 0, la dixième sera .
Pour faire du gris, les paramètres r, g, b doivent être identiques, d'où : c=color(b*28,b*28,b*28).
c=color(255-b*28,255-b*28,255-b*28)
Exercice
Les couleurs orangées du thème NumWorks respectent les proportions suivantes : rouge 100%, vert 75%, et bleu 25%. Reprendre l'exercice en présentant un dégradé de 10 bandes verticales orangées sous la mire de gris précédente.

Indication : il suffit de modifier dans le script précédent la plage des lignes y, ainsi que les arguments g et b de la fonction color (r,g,b).
Conclusion
On a vu le principe de codage des couleurs d'une image de petite dimension. A raison de 256 niveaux possibles pour chacune des 3 couleurs de base, il faut 3 octets par pixel, et davantage si l'on encode par exemple plus de 1000 niveaux par couleur (on parle de profondeur de couleur). Ce nombre d'octets est à multiplier par le nombre de pixels de l'image, ce qui peut facilement nécessiter plus de 10 Mo par image.
On dispose alors de procédés de compression d'images consistant à :
-
Indiquer par exemple que n pixels qui se suivent ont la même couleur (inutile de tous les coder) ;
-
Faire une table des couleurs présentes dans l'image (on crée une palette) et à coder pour chaque pixel l'emplacement de sa couleur dans la table ;
-
Faire des approximations : on utilise la même couleur pour des couleurs voisines.