
Gabriel Ozouf — 14 de outubro de 2021
A janela automática
Antes da versão 15.3.0, as curvas da aplicação Funções eram muito bem desenhadas, mas por vezes o zoom aplicado deixava um pouco a desejar. Para fazer face a este problema, tivemos de desenvolver um algoritmo capaz de calcular uma janela adaptada a cada função.
Problemas de escala
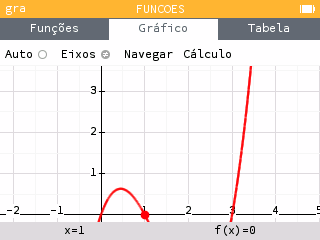
Uma representação gráfica de uma função é uma poderosa ferramenta pedagógica para um aluno que está a descobrir a matemática. Permite ao aluno familiarizar-se com as noções de análise, explorar os diferentes tipos de funções e descobrir as suas propriedades. Tomemos por exemplo um aluno que deseja ter uma ideia do comportamento da função f(x)=x(x-1)(x-3). Ao introduzir a expressão na aplicação Funções da nossa calculadora, com a versão 14 do software…
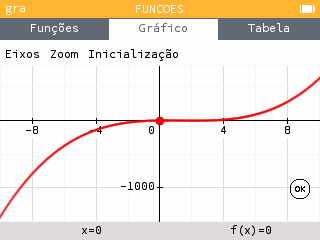
…apercebe-se de que a função é estritamente crescente, com um único zero?
Felizmente para nós, este aluno não esteve a dormir nas aulas de Matemática e sabe perfeitamente que esta função não é monótona. A sua calculadora enganou-o? O gráfico está a dizer a verdade, mas o zoom escolhido não faz justiça a este polinómio de terceiro grau… Não seria melhor se a janela proposta fosse mais parecida com esta?
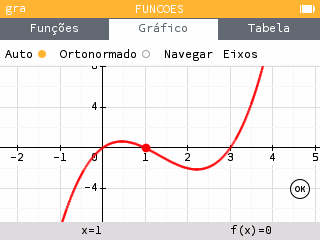
Um algoritmo demasiado simples
Como é que a calculadora decidiu esta janela, claramente pouco otimizada, para exibir a curva?
Até à versão 14, o algoritmo utilizado era muito simples. Por defeito, o eixo horizontal era -10 a 10 e o eixo vertical era escolhido para mostrar toda a curva.
Na primeira imagem, os limites do eixo y são portanto os valores extremos da curva, aqui f(-10)=-1430 e f(10)=630.
Sabendo que os extremos locais da função têm valores da ordem da unidade, não é surpreendente que sejam completamente invisíveis.
Para a versão 15, decidimos atualizar o nosso gráfico para que fosse capaz de fazer zoom nas curvas de uma forma muito mais inteligente.
Este é um problema complexo, porque a ideia subjacente é bastante subjetiva: o que torna uma parte da curva mais interessante que outra? E, sobretudo, como pode esta noção ser traduzida para uma linguagem matemática?
O primeiro passo foi, portanto, compilar uma lista de funções comuns, cada uma com o zoom que o utilizador esperaria. Esta lista foi utilizada para validar a nossa solução, assegurando que os zooms que propõe não se desviam demasiado dos procurados.
Como ilustrado no exemplo da introdução, a melhor janela concentra-se frequentemente nas variações da curva. Com esta noção como ponto de partida, pode-se listar os diferentes tipos de pontos de interesse que se deseja exibir no ecrã: zeros, mínimos e máximos e assíntotas verticais e horizontais.
Em busca dos pontos de interesse
O primeiro passo na construção da melhor forma de exibir uma curva cartesiana é, portanto, encontrar os pontos de interesse da função.
Para algumas categorias de curvas, a procura de zeros ou extremos é um problema já resolvido, particularmente no caso de polinómios com um grau mais pequeno. Mas, de um modo geral, não existe um método formal para resolver este problema, pelo que já ficaríamos satisfeitos com uma solução aproximada.
Poder-se-ia pensar que esta questão está bem documentada, e a literatura é de facto abundante quando o assunto se trata de encontrar zeros ou extremos num dado intervalo finito. Mas a informação é bem mais escassa quando o intervalo é o conjunto dos números reais.
É comum um algoritmo, na procura de zeros ou extremos, percorrer o intervalo selecionado calculando alguns dos valores da função para abcissas espaçadas regularmente. Para adaptar este esquema ao conjunto dos números reais, utilizamos uma progressão geométrica em vez de uma aritmética. Esta ideia baseia-se na seguinte observação: para a maioria das funções que encontramos, a distância entre dois pontos de interesse é frequentemente da mesma ordem de grandeza que as abcissas dos próprios pontos de interesse. Podemos, portanto, estudar a função pormenorizadamente em torno do zero e explorar as suas variações para abcissas maiores, num tempo razoável.
Na função f introduzida anteriormente, encontramos cinco pontos de interesse (três zeros e dois extremos locais), todos contidos no intervalo[0, 3]. Adiciona-se então uma margem para melhor centrar a curva, dando um intervalo horizontal em torno de [-2, 5].
Segunda dimensão
O segundo passo será determinar o intervalo exibido no eixo das ordenadas.
Investiguemos primeiro se é possível criar um quadro de referência ortonormado mais natural.
Uma vez que já conhecemos o intervalo horizontal e a proporção do ecrã, podemos deduzir o tamanho do intervalo vertical.
Para a função f, se o ecrã tiver uma proporção de 60%, precisamos de encontrar um intervalo vertical de tamanho (5 - (-2)) x 60% ou seja 4.2.
Resta-nos determinar a sua posição. Para tal, calculamos uma amostra aleatória dos valores da função. Procuramos um intervalo, de tamanho fixo, que contenha o número máximo destes valores, verificando ao mesmo tempo se os pontos de interesse encontrados anteriormente pertencem a este intervalo.
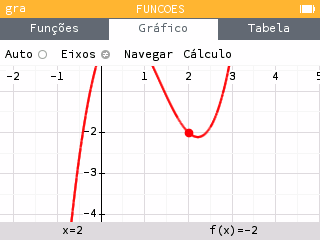
Uma janela demasiado baixa em relação à curva
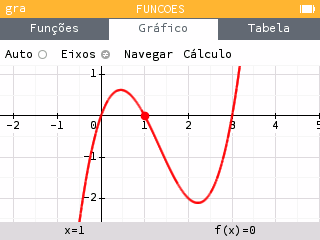
Uma janela que maximiza a porção da curva exibida
Uma janela demasiado alta em relação à curva
Por vezes não é possível construir uma estrutura de referência ortonormada satisfatória, por exemplo porque o tamanho do intervalo vertical não é suficiente para exibir todos os pontos de interesse.
Consideremos por exemplo a função 2f, que tem portanto as mesmas variações que f. O seu máximo local é 1.3, e o seu mínimo é -4.2. É portanto impossível exibir estes dois valores simultaneamente num intervalo vertical de tamanho 4.2…
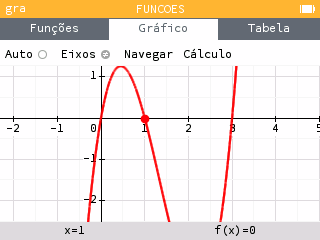
O mínimo e o máximo da curva não podem estar presentes ao mesmo tempo no ecrã com eixos de referência ortonormados
Neste caso, calculamos uma medida da ordem de grandeza da função, a média do logaritmo do seu valor absoluto. Esta medida de grandeza indica se a função toma os seus valores em dezenas, centenas, milhares… Não exibimos valores demasiado grandes em relação ao tamanho médio. Isto permite, por exemplo, cortar os ramos divergentes das curvas polinomiais: se fossem incluídos na janela, o seu crescimento muito rápido esmagaria o resto da curva. É isto que acontece no exemplo introdutório.
Uma questão de comprimisso
O algoritmo de zoom automático na versão 15 do Epsilon é consideravelmente mais complexo do que o algoritmo básico que utilizámos anteriormente, pelo que é também muito mais instável.
Um algoritmo simples terá um comportamento previsível, tanto nos seus sucessos como nos seus fracassos. Quando o procedimento para exibir uma curva é simplesmente desenhar todos os seus valores entre -10 e 10, o algoritmo vai falhar sempre da mesma maneira.
Em contrapartida, com o novo método, multiplicam-se o número de bugs, casos especiais e parâmetros a ter em conta.
O eixo horizontal pode não exibir um extremo se o passo entre valores utilizado na pesquisa for demasiado grande, mas o processo pode ser demasiado lento se o passo for muito pequeno. A procura de uma janela de referência ortonormada pode ser defeituosa se a função for demasiado regular: o algortimo não pode escolher o melhor intervalo, porque são todos igualmente importantes. O cálculo da média logarítmica pode tornar-se inútil se os valores da função forem demasiadas vezes zero. E algumas curvas simplesmente não têm pontos de interesse e devem ser reduzidas a um intervalo por defeito…
Mas o trabalho não fica por aqui, uma vez que as novas capacidades do gráfico levaram-nos a repensar completamente a interface da nossa aplicação de Funções!
A aplicação final é uma ferramenta muito mais prática para os utilizadores, mesmo que o preço a pagar seja um software um pouco mais caprichoso para nós, programadores.

Gabriel Ozouf — Engenheiro de Software
O Gabriel juntou-se à NumWorks em 2020, como Engenheiro de Software. Se a calculadora está a melhorar todos os dias com novas funcionalidades, é em grande parte graças a ele. Apesar de todos os seus sucessos, o Gabriel manteve a cabeça fria graças ao termóstato no escritório, que regula rigorosamente para 18°C!

