De vensterinstellingen van een curve

Vóór de update naar versie 15.3.0, waren de curven in onze functies applicatie zeer mooi getekend, maar de zoominstelling liet soms te wensen over. Om dit probleem op te lossen, moesten wij een algoritme ontwikkelen waarmee voor elke functie een geschikt venster kon worden berekend.

Problemen met verhoudingen

Een grafiek is een krachtig leermiddel voor een leerling die wiskunde aan het ontdekken is. Het helpt hen vertrouwd te raken met het analyseren van verschillende soorten functies en de specifieke eigenschappen daarvan te ontdekken. Neem het voorbeeld van een leerling die de volgende functie wil verkennen: f(x)=x(x-1)(x-3). Bij het invoeren van deze uitdrukking in de Functies applicatie met versie 14 van onze software…

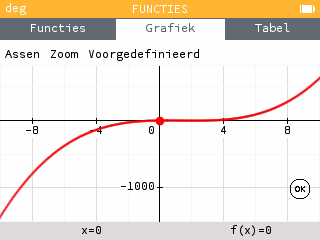
… denkt de leerling dat deze functie een enkel stijgend verloop heeft met slechts één nulpunt?

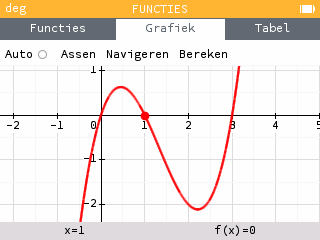
Gelukkig voor ons heeft deze leerling niet zitten slapen tijdens de wiskundelessen en weet dat deze functie andere eigenschappen heeft. Liegt de rekenmachine dan tegen deze leerling? De grafiek wordt wel correct weergegeven, maar de gekozen zoom doet geen recht aan deze derdegraads polynoom… Zou het niet beter zijn als het voorgestelde venster er meer zoals dit uitzag?

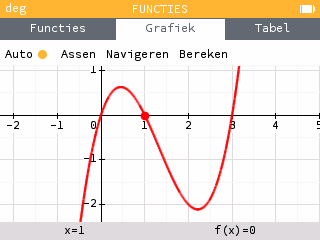
Een iets te simpel algoritme

Hoe heeft de rekenmachine besloten om de curve weer te geven op dit bepaald niet optimale venster?

Tot versie 14 werd er een zeer eenvoudig algoritme gebruikt. Standaard liep de horizontale as van -10 tot 10, en de verticale as werd gekozen om de hele curve weer te geven.

Op de eerste afbeelding zijn de grenzen van de y-as daarom de extreme waarden van de kromme, in dit geval f(-10)=-1430 en f(10)=630.
Gezien de orde van grootte van de lokale extremen van de functiewaarden, is het niet verwonderlijk dat zij volledig onzichtbaar zijn.

Voor versie 15 hebben we besloten om dit algoritme te verbeteren zodat we op een veel slimmere manier in kunnen zoomen op de curve.

Dit is een ingewikkeld probleem, omdat het onderliggende idee nogal subjectief is: wat maakt het ene deel van een curve interessanter dan het andere? En vooral, hoe kan dit begrip in wiskundige taal worden vertaald?

De eerste stap was daarom om een lijst van gemeenschappelijke functies samen te stellen, en te definiëren wat de zoom moet zijn die de gebruiker zou verwachten. Deze lijst is gebruikt om onze oplossing te valideren, door ervoor te zorgen dat de weergegeven venster instellingen niet te veel afwijken van de gewenste.

Zoals in het inleidende voorbeeld wordt geïllustreerd, is het beste venster vaak gericht op de variaties van de curve. Als we dit als uitgangspunt nemen kunnen we een lijst maken van de verschillende soorten aandachtspunten die we op het scherm wensen weer te geven: nulpunten, minima en maxima, verticale en horizontale asymptoten.

Op zoek naar interessante punten

De eerste stap bij het construeren van een referentiekader voor de weergave van een cartesische kromme is het vinden van de interessante punten van de functie.

Voor sommige type krommen is het zoeken naar nulpunten of extrema’s een probleem dat reeds is opgelost, vooral in het geval van polynomen van lage graad. Maar in het algemeen bestaat er geen formele methode om dit probleem op te lossen, zodat we ons tevreden moeten stellen met een benaderende oplossing.

Men zou kunnen denken dat deze vraag ook goed gedocumenteerd is, en de literatuur is inderdaad overvloedig over het onderwerp van het vinden van nulpunten of extrema in een gegeven eindig interval. Maar de documenten zijn zeldzamer wanneer dit interval over de verzameling van reële getallen gaat.

Het komt veel voor dat een zoekalgoritme voor nulpunten of extrema’s het interval doorkruist door waarden van de functie te berekenen, bij regelmatig verdeelde x-coördinaten. Door opeenvolgende waarden te vergelijken, kunnen we te weten komen of de functie van teken of veranderingsrichting verandert. Om dit schema aan te passen aan de verzameling van reële getallen, gebruiken wij een meetkundige aanpak in plaats van een rekenkundige. Dit idee is gebaseerd op de volgende waarneming: voor de meeste functies die we zijn tegengekomen, is de afstand tussen twee interessante punten vaak van dezelfde orde van grootte als het x-coördinaat van de interessante punten zelf. Wij kunnen dus de functie fijn rond nul bestuderen en haar variaties voor grote x-coördinaten onderzoeken in een redelijke hoeveelheid tijd.

Op de eerder ingevoerde functie f vinden wij vijf interessante punten (drie nulpunten en twee lokale extrema), allen gelegen in het interval [0, 3]. Er wordt een marge toegevoegd om de curve beter te centreren, hetgeen een horizontaal interval rond [-2, 5] oplevert.

Tweede dimensie

De tweede stap is het bepalen van het interval dat op de Y-as wordt weergegeven.

We kijken eerst of het mogelijk is een natuurlijker referentiekader te creëren met gelijke assen. Aangezien wij reeds het horizontale interval en de beeldschermverhouding kennen, kunnen wij de grootte van het verticale interval afleiden. Voor de functie f, als het scherm een verhouding heeft van 60%, moeten we een verticaal interval vinden van grootte (5 - (-2)) x 60% = 4.2

We moeten nu alleen nog zijn positie bepalen. Daartoe berekenen wij steekproefsgewijs de waarden van de functie. Hierbij zoeken wij het interval van vaste grootte dat het maximum aantal van deze waarden bevat, en we gaan na of de eerder gevonden interessante punten tot dit interval behoren. Op deze manier construeren wij het venster dat de ruimte die de kromme op het scherm inneemt, zo groot mogelijk maakt.

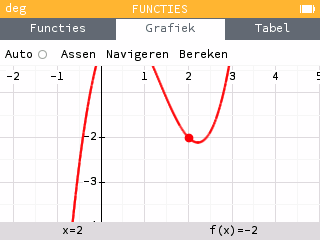
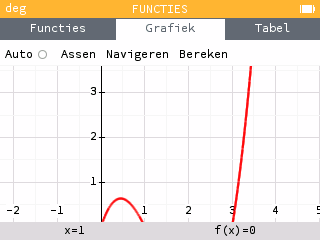
Soms is het niet mogelijk een geschikt venster met gelijke assen weer te geven, bijvoorbeeld omdat de grootte van het verticale interval niet voldoende is om alle interessante punten weer te geven. Neem bijvoorbeeld de functie 2f, die dus dezelfde variaties heeft als f. Het bereikt op zijn lokale maximum ongeveer 1.3, en op zijn lokale minimum ongeveer -4.2. Het is dus onmogelijk deze twee waarden gelijktijdig weer te geven met een verticaal interval van grootte 4.2…

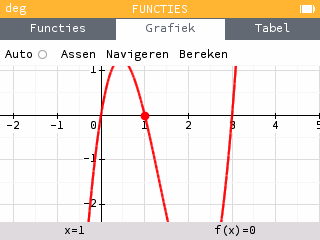
In dit geval berekenen wij een maatstaf voor de orde van grootte van de functie, het gemiddelde van de logaritme van de absolute waarde. Deze hoeveelheid geeft aan of de functie zijn waarden in de tientallen, honderdtallen, duizendtallen… We geven geen waarden weer die te groot zijn in verhouding tot de gemiddelde grootte. Dit maakt het bijvoorbeeld mogelijk de divergerende takken van polynomiale krommen af te snijden; indien zij in het venster zouden worden opgenomen, zou hun zeer snelle groei tot gevolg hebben dat de rest van de kromme wordt platgedrukt. Dit is wat er gebeurt in het inleidende voorbeeld.

Een kwestie van compromissen

Het algoritme voor de automatische zoom in Epsilon versie 15 is aanzienlijk complexer dan het basis algoritme dat we eerder gebruikten, waardoor het ook instabieler is.

Een eenvoudig algoritme zal voorspelbaar gedrag vertonen, zowel in zijn successen als in zijn mislukkingen. Wanneer de procedure om een kromme weer te geven simpelweg bestaat uit het tekenen van alle waarden tussen -10 en 10, mislukt dit altijd op dezelfde manier.

Omgekeerd wordt met de nieuwe methode het aantal bugs, speciale gevallen en parameters waaruit kan worden gekozen, verveelvoudigd. Een lange horizontale as kan bijvoorbeeld een extreme waarde missen als de stapgrootte te groot is, maar kan ook veel te kort zijn als diezelfde stapgrootte te klein is. Ook het zoeken naar een venster met gelijke assen heeft zijn limitaties als de functie te regelmatig is: het algoritme kan dan niet het beste interval kiezen omdat de waarden allemaal even belangrijk zijn. De berekening van het logaritmisch gemiddelde kan nutteloos worden als de waarden van de functie te vaak nul zijn. En sommige krommen hebben gewoon geen punten van belang en moeten worden teruggebracht tot een standaard interval…

Er is nog genoeg werk te doen dus, want de nieuwe mogelijkheden van het algoritme hebben geleid tot een volledige herziening van de interface van onze Functies-applicatie!

Hoewel dit ingewikkelde algoritme het werk uitdagender maakt voor onze programmeurs, is het eindresultaat een veel praktischer instrument voor de gebruikers geworden.