Croissance bactérienne
Suites numériques Fonction exponentielle Fonction logarithme Outils de régression
Objectif
Etablir l'équation du modèle exponentiel de croissance bactérienne à partir de la manipulation de données expérimentales.
On considère une bactérie en phase de croissance, présente initialement en quantité , qui se divise pendant un temps . Cela signifie qu'à chaque division, la cellule-mère se scinde en deux cellules-filles.
-
On s'intéresse à l'évolution de la population de bactéries.
-
Combien compte-t-on de bactéries après une génération (ou division) ? Après deux générations ?
-
Quelle est la relation entre , le nombre de bactéries au bout de générations, et , le nombre de bactéries initial ?
Après une génération, on compte bactéries. Au bout de deux générations, on en compte car la population a encore doublé.
On reconnaît une suite géométrique de raison 2, d'où
-
-
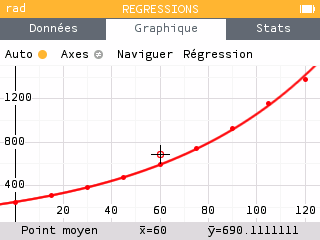
Entrer ces données dans l'application Régressions, et vérifier que les données suivent bien une croissance exponentielle en sélectionnant le modèle de régression adapté.
Pour choisir un modèle de régression, il suffit d'accéder à l'onglet Graphique puis d'appuyer sur la touche ok.
-
On appelle le taux de croissance des bactéries, c'est-à-dire le nombre de divisions par unité de temps. On a donc et .
Montrer que :
-
D'après cette expression, conjecturer la représentation graphique de en fonction de .
-
On propose de réaliser une nouvelle régression en représentant maintenant en fonction de .
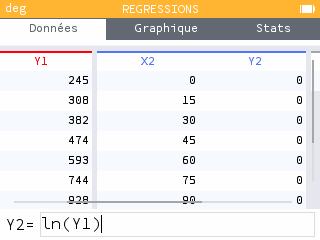
Dans l'onglet Données de l'application, nous allons réutiliser les mêmes valeurs en X1 et en X2 : on sélectionner la cellule X2, toucke OK, puis
Remplir avec une formule > Vide. En appuyant sur la touche var, on retrouve dans le sous-menu Listes les données de la colonne X1 afin d'entrerX2=X1.Pour les valeurs de Y2, nous allons réutiliser les valeurs de Y1 en appliquant le même procédé avec un logarithme. On sélectionne Y2, touche OK, remplir avec une formule :
Y2 = ln(Y1).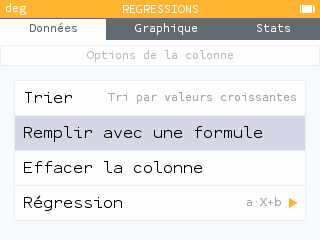
Désactiver les données du premier tableau (en sélectionnant la cellule X1, touche OK puis décocher
Afficher la série) et vérifier votre conjecture en effectuant une régression sur les données du second tableau.Une fois la courbe de régression affichée, appuyer sur ok pour obtenir des informations complémentaires. Quelle est la valeur du coefficient directeur à 10-3 près ?
-
En déduire une expression de .
-
Quelle est la limite de la fonction lorsque tend vers ? Ce modèle mathématique est-il cohérent pour décrire toute la dynamique de croissance des bactéries dans un milieu donné ?
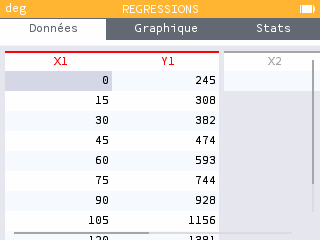
Voici les données expérimentales qui ont été recueillies. On donne en minutes et le nombre de bactéries en milliers :
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | |
| N | 245 | 308 | 382 | 474 | 593 | 744 | 928 | 1 156 | 1 381 |
On sait que d'où .
L'expression est de la forme donc sa représentation graphique sera vraisemblablement une droite de coefficient directeur et d'ordonnée à l'origine .
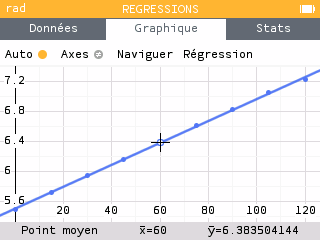
On obtient un coefficient directeur égal à 0,015.
avec .
D'où
La limite de la fonction est infinie. Cela impliquerait que les bactéries se divisent à l'infini, ce qui n'est ni vrai, ni possible. En effet, les bactéries nécessitent un certain nombre de ressources pour survivre et se diviser. Or, les ressources en un milieu donné ne sont pas illimitées, elles vont finir par manquer et, sans apport extérieur, la croissance des bactéries va ralentir puis la population, décliner.
Ce modèle ne permet de décrire qu'une phase du processus de croissance des bactéries : la phase dite de croissance exponentielle.