Datation archéologique

On considère un échantillon de matière organique. Celui-ci contient à l'instant $t\,\left(t \geq 0 \right)$, $N\left( t \right)$ noyaux radioactifs.

1. On sait que la vitesse de désintégration des noyaux $N'\left( t \right)$ est décroissante et proportionnelle (de coefficient $\lambda$ positif et non-nul) au nombre de noyaux radioactifs. Établir l'équation différentielle correspondante.

   La fonction est décroissante, donc la dérivée est négative, d'où :

   $N'\left(t\right)=-\lambda N\left(t\right)$

2. On considère qu'à l'instant $t=0$, le nombre de noyaux radioactifs est égal à $N_{0}$. Résoudre l'équation différentielle.

   Il s'agit d'une équation différentielle du premier ordre à coefficient constant dont la solution est de la forme $C\mathrm{e}^{-\lambda t}$ avec $C$ constante. Pour trouver la valeur de cette constante, on s'intéresse aux conditions initiales :

   $\displaystyle N\left(0\right)=C\mathrm{e}^{0}=C=N_{0}$

   D'où :

   $\displaystyle N\left( t \right) = N_{0}\,\mathrm{e}^{-\lambda t}$

3. Le temps de demi-vie $t_{\frac{1}{2}}$ est définie comme étant le temps au bout duquel le nombre de noyaux radioactifs est divisé par deux. Etablir l'équation correspondante et en déduire une expression de $t_{\frac{1}{2}}$.

   $\displaystyle N\left(t_{\frac{1}{2}}\right) = \frac{N_{0}}{2} \iff \mathrm{e}^{-\lambda t_{\frac{1}{2}}} = \frac{1}{2} \iff t_{\frac{1}{2}}=\frac{\ln{2}}{\lambda}$

4. Établir une expression afin de connaître l'âge d'un échantillon radioactif en fonction de sa demi-vie et de son nombre de noyaux radioactifs à l'instant $t$.

   On cherche $t \left( t \geq 0 \right)$ tel que :

   $\displaystyle N\left(t\right)=N_{0}\,\mathrm{e}^{-\frac{\ln{2}}{t_{1/2}}t} \iff -\left(\frac{\ln{2}}{t_{1/2}} \right)t = \ln\left({ \frac{N \left( t \right)} {N_{0}}}\right) \iff t = - \ln\left( {\frac {N \left( t \right)} {N_{0}}} \right) \times \left( \frac{t_{1/2}}{\ln{2}} \right)$

   On pourra faire remarquer que l'expression $\displaystyle \frac {N \left( t \right)} {N_{0}}$ est inférieure à 1, d'où un logarithme négatif mais une expression globalement positive.

5. On s'intéresse à un échantillon organique qui comprend $7,00 \times 10^{6}$ noyaux radioactifs. Initialement, il en contenait $1,00 \times 10^{8}$. Quel est l'âge de cet échantillon ? On rappelle que le temps de demi-vie du carbone 14 est de 5730 ans.

   

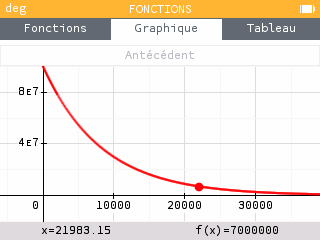
   En utilisant l'expression précédente, on obtient :

   $\displaystyle t = - \ln\left( {\frac {7,00\times 10^{6}} {1,00 \times 10^{8}}} \right) \times \left( \frac{5730}{\ln{2}} \right) = 2,20 \times 10^{4}$

   L'échantillon est donc âgé d'environ 22 000 ans.